Chapter
3
1st
Degree Polynomial Equations
ax+b=0
3.1.
The Equation ax+b=0
Let's see how we
solve the above equation with the help of the properties of the operations,
for the various values of a,b.
We have ax+b = 0
<=> ax+b - b = - b <=> ax = - b
Now we distinct the
following possibilities:
A. If 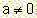 the equation has exactly one solution. That is:
the equation has exactly one solution. That is: 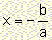
B. If a=0 the
equation becomes 0x = - b and:
B1. If 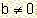 the equation does not have a solution in R.
the equation does not have a solution in R.
B2. If b=0 the equation takes the form 0x=0, which is true
for every 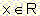
Our conclusions can be summarized in the
table bellow:
If 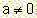
|
It has unique solution
|
If a=0 and 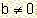
|
It is has no solutions in R
|
|
If a=0 and b=0
|
It is true for every 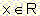
|
The solution of an equation, that is the
procedure that we follow in order to solve an equation is an algorithm.
Its steps can be seen in the following example:
Example
Solve the equation: 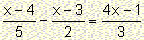
Solution
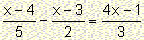 <=>
<=>
<=> 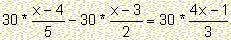 <=>
<=>
| Step 1: We eliminate the
denominators multiplying the terms of the equation with the lowest common
multiple of the denominators. |
<=> 6(x-4) - 15(x-3) = 10(4x-1) <=>
|
Step 2: Applying the
distributive law a(b+c)=ab+ac we eliminate the parenthesis
|
<=> 6x - 24 - 15x +45=40x - 10 <=>
|
Step 3: We take all
the unknown terms to the one side and the known terms to the other side
|
<=> 6x - 24 -15x + 45 = 40x - 10 <=>
|
Step 4: We do the relevant
operations
|
<=> -49x = -31 <=>
|
Step 5: We divide both
sides by the factor of the unknown variable(here -49)
|
<=> x = -31/-49 <=> 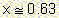
We have to make clear the following:
-
The reason for doing all the above is to isolate
the unknown variable x at the one side of the equation in order the equation
to take the form ax=b
-
The transfer of one term from the on side
of the equation to the other is achieved with the addition of the opposite
term of the one that we want to transfer. So, when we distinguish the known
from the unknown terms, during the transfer from the one side of the equation
to the other, the signs of the terms that we transfer change.
-
Taking all the unknown variables in the same
side of the equation is achieved with the help of the distributive law
eg. 6x - 15x - 40x = -49x






the equation has exactly one solution. That is:
the equation does not have a solution in R.
<=>
<=>