Chapter 4
The Binomial Equation
 


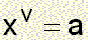
The case where a = 0 has obvious solution and therefore it is not considered in this chapter.  
 
4.1 The binomial equation were x and a real numbers 

A)    Consider the equation .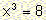
        This equation has exactly one positive solution: 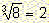, according to the definition of the root of a
        non negative number. The equation does not have any negative solutions because for 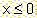 it is
 .
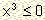        Therefore the equation has a unique solution, that is .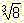
        In general:
 
The equation 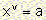 with v being an odd number and a>0, has exactly one solution: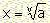  
 
    For example:

B)    Consider the equation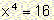 
        Thinking like before we conclude that the equation has one positive solution: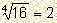 
        We observe though that  the number 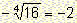solves the equation as well.
        So, the equation has two exactly solutions which are: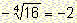 
        In general:
 
The equation 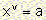with v even and a>0 has exactly two solutions, which are: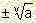 
    For example: C)    Lets consider the equation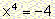 
        It is obvious that this equation has no solutions in R, since as we know 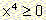 for every x in R.
        In general:
 
The equation 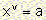with v even and a<0 has no solutions in R.
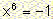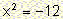    For example: D)    Consider the equation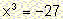 
        I have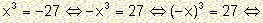 
        
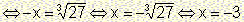
        In general:
 
The equation 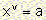with v odd and a<0 has exactly one solution: 
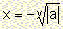
        For example: